Computing Bezier Curve
CIS 5150-001 Fundamentals Of Linear Algebra And Optimization:
In this project, I explored how linear algebra underpins the computation of Bézier curves. While many tools let you draw curves visually, understanding the mathematics behind them gives deeper control and insights—especially useful for computational designers using Rhino + Grasshopper.
Derived the Bézier curve formula in terms of linear combinations of control points and basis polynomials.
Implemented the curve computation from scratch, applying matrix operations to evaluate points along the curve.
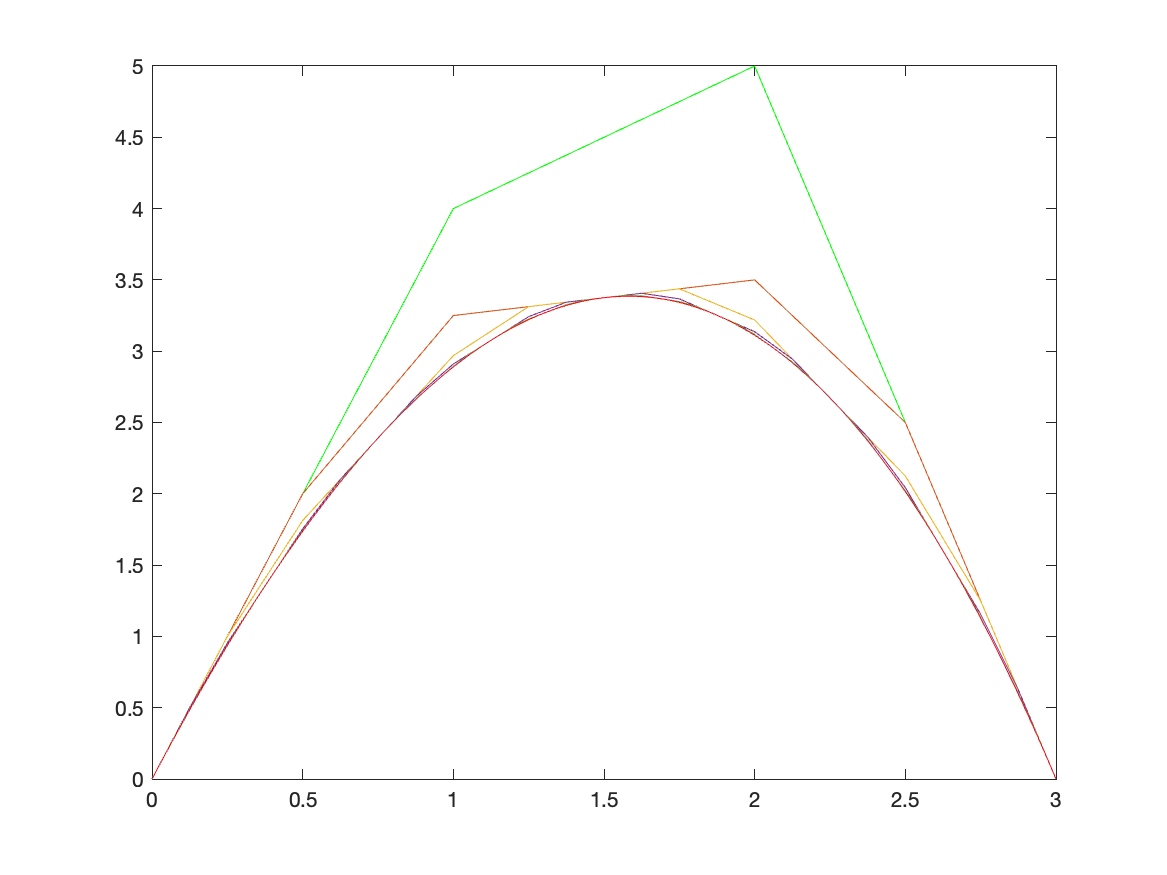
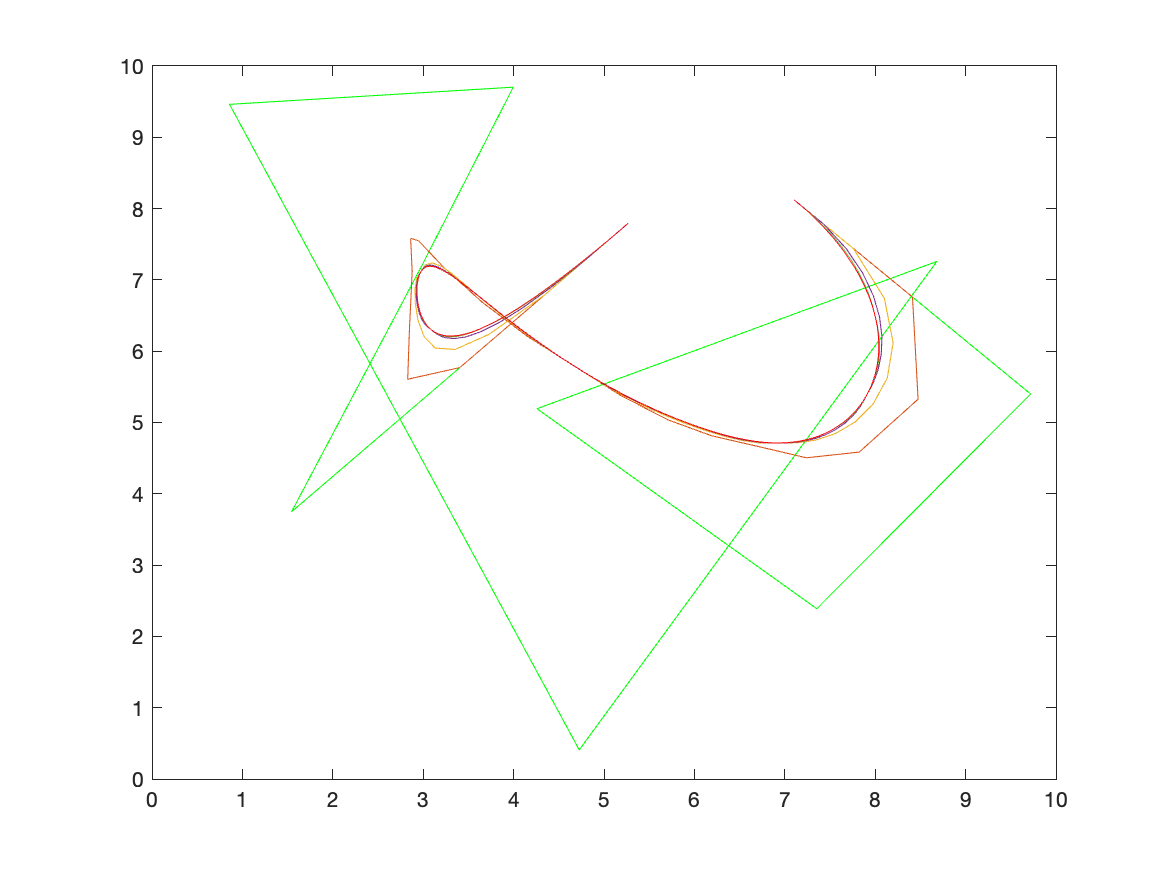
Visualized intermediate control polygons, sampled points, and the resulting smooth curve.
Compared theoretical predictions with actual outputs, reflecting on sources of deviation (e.g. numerical approximation, sampling density).
Bézier curves are foundational in design, modeling, and computer graphics. A clear understanding lets designers manipulate shapes more precisely.
Institution: University of Pennsylvania
Class: CIS 5150 Fundamentals Of Linear Algebra And Optimization
Instructor: Jean Gallier
In Collaboration with: Blake Hernandez, Hongshuo Zhou
We have proven the required properties of the second derivatives for cubic Bézier curves and derived the modified tridiagonal linear system under the natural end conditions. This system allows us to compute the de Boor control points necessary to construct a smooth, C² continuous cubic spline that interpolates the given data points.